4915. Дерево

Дано взвешенное дерево. Найдите кратчайшее расстояние между заданными парами вершин.

Вход. Первая строка содержит количество вершин n (1 ≤ n ≤ 150000) в дереве. Вершины нумеруются целыми числами от 0 до n – 1. В следующих n – 1 строках содержатся три целых числа u, v, w, где w (0 ≤ w ≤ 1000) – вес ребра, соединяющего вершины u и v. Далее идет целое число m (1 ≤ m ≤ 75000) – количество запросов. В каждой из следующих m строк содержатся два числа – номера вершин, между которыми следует найти расстояние.

Выход. Для каждого запроса выведите в отдельной строке одно число – искомое расстояние.

Пример входа	Пример выхода
3 1 0 1 2 0 1 3 0 1 0 2 1 2	1 1 2

РЕШЕНИЕ

структуры данных – Least Common Ancestor

Анализ алгоритма

Под весом ребра будем понимать его длину. Запустим поиск в глубину из корня дерева, чтобы для каждой вершины x определить расстояние dist[x] от нее до корня.

Рассмотрим запрос (u, v), в котором следует найти расстояние между вершинами u и v. Найдем их наименьшего общего предка: пусть l = LCA(u, v). Тогда искомое расстояние равно

dist[u] – dist[l] + dist[v] – dist[l] =

dist[u] + dist[v] – 2 * dist[l];

Пример

Дерево из условия задачи имеет вид:

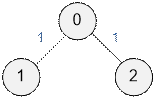
Рассмотрим другой пример. Пусть вес каждого ребра дерева равен 1. Возле каждой вершины x запишем значение dist[x].

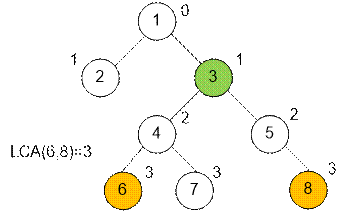
Вычислим расстояние между вершинами 6 и 8. Поскольку LCA(6, 8) = 3, расстояние между 6 и 8 равно

dist[6] + dist[8] – 2 * dist[3] = 3 + 3 – 2 * 1 = 4

Реализация алгоритма

Дерево храним в виде взвешенного графа в списке смежности g. Для неориентированного ребра (u, v) с весом w в g[u] хранится пара (v, w), а в g[v] – пара (u, w).

Метки d и f (время входа и выхода из вершины) необходимы для быстрого определения отношения “является предком” для двух вершин.

В ячейке dist[i] хранится расстояние от корня до вершины i.

Массив up используется для нахождения наименьшего общего предка (LCA) методом двоичного подъема.

#define MAX 500001

vector<pair<int,int> > g[MAX];

int d[MAX], f[MAX], dist[MAX];

int up[MAX][20];

Функция dfs выполняет поиск в глубину в дереве, начиная с вершины v. Родительской вершиной для v является p. Расстояние от корня дерева до v равно len. При обходе дерева в глубину можно обойтись без использования массива посещенных вершин used. Достаточно для каждой вершины v хранить ее предка p, чтобы в процессе обхода избежать возвращения из v в p.

void dfs (int v, int p = 0, int len = 0)

{

d[v] = timer++;

up[v][0] = p; dist[v] = len;

for(i = 1; i <= l; i++)

up[v][i] = up[up[v][i-1]][i-1];

for (auto x : g[v])

{

int to = x.first;

int dist = x.second;

if (to != p) dfs(to, v, len + dist);

}

f[v] = timer++;

}

Функция Parent возвращает true, если вершина a является предком вершины b.

int Parent(int a, int b)

{

return (d[a] <= d[b]) && (f[a] >= f[b]);

}

Функция LCA возвращает наименьшего общего предка для двух вершин a и b, используя метод двоичного подъема.

int LCA (int a, int b)

{

if (Parent(a, b)) return a;

if (Parent(b, a)) return b;

for (int i = l; i >= 0; i--)

if (!Parent(up[a][i], b)) a = up[a][i];

return up[a][0];

}

Основная часть программы. Читаем количество вершин n в дереве.

scanf("%d",&n);

Вычисляем l = .

l = 1;

while ((1 << l) <= n) l++;

Заносим дерево в список смежности g.

for(i = 0; i < n - 1; i++)

{

scanf("%d %d %d",&u,&v,&w);

g[u].push_back({v,w});

g[v].push_back({u,w});

}

Запускаем поиск в глубину из корня дерева – вершины 0.

dfs(0);

Обрабатываем m запросов. Для каждой пары вершин u и v выводим расстояние res между ними.

scanf("%d",&m);

for(i = 0; i < m; i++)

{

scanf("%d %d",&u,&v);

lca = LCA(u, v);

res = dist[u] - dist[lca] + dist[v] - dist[lca];

printf("%d\n",res);

}